ケプラーの火星楕円軌道
≪ケプラーはいかにして火星の楕円軌道を発見したか≫
いまや小学生でも知っている地動説は、コペルニクス(1473~1543)以後の近代の所産である。もちろん太陽中心の宇宙体系は古代ギリシャのヘラクレイデス(B.C.390~310)やアリスタルコス(B.C.310~250)がすでに気づいていた。とくにアリスタルコス(B.C.310~250)は観測と計算より「地球の300個分の大きさを持つ太陽がちっぽけな地球の周りをまわるなんてことがあるだろうか、むしろその逆のほうが自然なのではないか?」 として太陽の周りをまわる地球を考えていたといわれる。
しかし、ヒッパルコス(B.C.160~125)やプトレマイオス(83年頃~168)は彼らの説を退ける。それは惑星運動の詳細、とくに軌道が楕円であることからくる偏差<中心差>をうまく説明できなかったからである(ほかに年周視差の問題もあるが)。その偏差をうまく説明したのが<離心円>とプトレマイオスが導入した<エカント(Equant)>であった。この二つの概念の導入によって惑星の運動が極めてうまく説明できるようになる。それゆえに、ヒッパルコス・プトレマイオスの宇宙観は1500年もの長い間信奉されてきた。
離心アノマリー
ケプラーが楕円軌道を発見した火星軌道(離心率 e=0.0934)の場合、長半軸 a=10cm とすると短半軸 b は
長半軸と短半軸との差は 0.5mm しかない。つまり円軌道をコンパスで描くと、楕円軌道はその線幅の中に埋もれてしまうことになる。
学校では火星軌道を楕円として極端に扁平した形で教えすぎるためにこのところがよく理解されていない。
(各惑星の離心率 水星 0.2056、金星 0.0068、地球 0.0167、火星 0.0934、木星 0.0485、土星 0.0555)
惑星の楕円軌道は円軌道とほとんど変わらない。だからプトレマイオスやコペルニクスにとって重要なのはその円軌道上を移動する惑星の前後の時間的な変動を説明することだった、のである。
一方楕円の中心と焦点との距離 c は
となり、1cm近くある。
地球の場合,10cm の円を描くと中心差は c=0.167
で真円と言っていいほどであるが、それでも離心アノマリー(中心差問題)は無視できない現象を引き起こす。例として地球と太陽を考えると太陽の運行がそれを示している。すなわち春分・夏至・秋分・冬至の間隔が等しくないということに表れているのである。
離心円
春分・夏至・秋分・冬至の間隔が等しくないことはグノーモンの観察より古代ギリシアの時代から知られていた。ヒッパルコスによると春分から夏至までは94日12時間、夏至から秋分までは92日12時間、秋分から冬至までは88日3時間、冬至から春分までは90日3時間である。そこでこのことを説明するのに考案されたのが<離心円>である。太陽は地球を中心とした円ではなく、地球とは異なる点を中心とした円=離心円
の上を等速で円運動していると考えた。
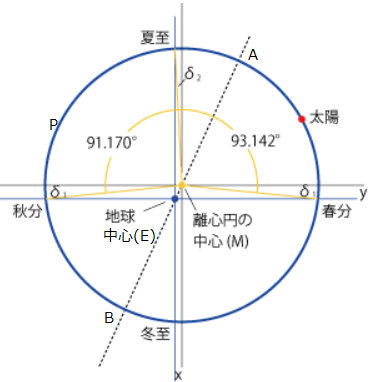
地球から見て春分・夏至・秋分の方向はそれぞれ90°間隔ですが、離心円の中心(M)から見た角度はそれとは異なります。
太陽は離心円上を等速で運動しますから、公転速度ω=360°÷365.25日です。Mから見た角度はこれに所要日数をかけて、春分と夏至のなす角度は93.142°、夏至と秋分のなす角度は91.170°となります。
Mから見た春分と秋分の方向のズレδ1は等しいので、
180°+2δ1=93.142°+91.170°
したがって、δ1=2.156°
夏至の方向のズレδ2は図より、
δ1+90°+δ2=93.142°
したがって、δ2=0.986°
地球と離心円の中心Mのズレ(x,y)は離心円の半径をRとすると、
x=R sinδ2、y=R sinδ1であり、
方向
=arctan(y/x)≒65.42°
距離Re
=
≒0.04137R
は太陽が地球からもっとも遠ざかる方向=遠地点A(遠日点)、その逆は太陽が地球にもっとも近づく方向=近地点B(近日点)です
と直交する方向に太陽が来るとき、Mから見た位置と地球から見た位置がもっとも大きくずれます。
ズレの大きさcは sin c = Re / R = eより、c≒2.37°です。地球の離心率から導かれる値は1.9°とみられているので、ヒッパルコスで計算すると若干大きい。
太陽が一定時間に動く角度はMから見れば等しくなりますが、地球から見た場合は角度が変化します。
近地点付近では地球から見た角度は大きくなる=速く動くように見えます。
遠地点付近では地球から見た角度は小さくなる=遅く動くように見えます
このように、離心円は楕円軌道に相当する役割を持っています。
さらに、離心円上の運動を、離心円の中心M に対してではなく、M をはさんで地球のちょうど反対側にある点に対して一様に運動すると仮定すれば、よりよい精度で楕円運動を近似することができます。
この、M をはさんで地球のちょうど反対側にある点のことを エカント と呼びます。
楕円軌道のアイデア
プトレマイオスの体系では太陽は一定の速度で円周上を移動していた。その円は地球とは中心を異にしているため、地球からはまるで太陽が速度を変えるように見える。同じようにコペルニクスの体系では地球が一定の速度で移動する。太陽は地球の周回円の中心にないため、まるで速度を変えて動くように見える。
そしてヨハネス・ケプラー(1571-1630)は、これは間違っていると考えた。「もし太陽に最も近い惑星である水星が一番速く動き、最も遠い惑星である土星が一番遅く動くのなら、それは水星が太陽に最も近いせいだ、近いために太陽のエネルギーを一番多く受け、それで自然に一番速く動くのだ、と。そこで地球は冬には夏より太陽に近づくので、冬の間、軌道上を実際早く移動するに違いない」と推論した。いうまでもないが、ケプラーは太陽は静止し、惑星はその周りを巡り動く、という地動説を信奉していた。静止する太陽が惑星を動かす、しかも惑星は太陽との距離を変えながら動く、すなわち太陽は惑星の円運動の中心にあるのではなく、さらに惑星は固有の力によって太陽に近づいたり遠ざかったりする。ケプラーの惑星軌道論は以上を原理として展開されている。
ケプラーは1599年、ティコ・ブラーエ (1546-1601)
に招かれ、プラハへと移った。ティコは当代きっての大観測家であり、1576年から1597年の21年間、デンマーク(現スウェーデン領)のヴェン島にウラニボリ天文台を建設して天空の観測を続け、さらにプラハでも観測を続けていたのであった。この観測データは望遠鏡のなかった当時、肉眼で観察されたものとしては最高の精度を持っていた。ティコは臨終の遺言で、16年におよぶ観測の資料の整理をケプラーに委託した。こうして観測家ティコの正確で膨大な観測データが理論家ケプラーの手に渡り整理・分析されたのである。しかし火星の離心率0.0934の楕円と、その楕円の長半軸とおなじ半径の円を描いてみて比較してみれば楕円と円の形の上での違いは、前述したようにほとんどないことが解る。だからティコ・ブラーエの観測データがいくら正確だったと言っても、直接楕円と円の形の違いを見極めて楕円軌道を発見することはできなかったであろう。
前置きが長くなりましたが、ここからいよいよケプラーのアイデアにはいります。
(半径が1の場合と100000の場合が混ざっています)
ケプラーは、観測データから三日月形の最も厚い部分の長さは 429 であることは分かったが、その意味するもの、そして三日月形になる原因について考えあぐねていたとき
「まったく偶然に最大の視覚的 均差を図り取った 5°18´という角度の正割 に思い至った。この値が100429であること を見たとき、まるで新たな光のもと、眠り から目覚めたかのように、以下の推論をし
始めた。平均的な長さを取る所で均差の視覚的部分が最大になる。平均的な長さを取る所で三日月形つまり距離の短縮分が最大になり、ちょうど最大の視覚的均差の正割 100429 が半径 100000
を上回る分になる。 したがって、平均的な長さを取る所で正割の代りに半径を用いると観測結果のとおりとなる」
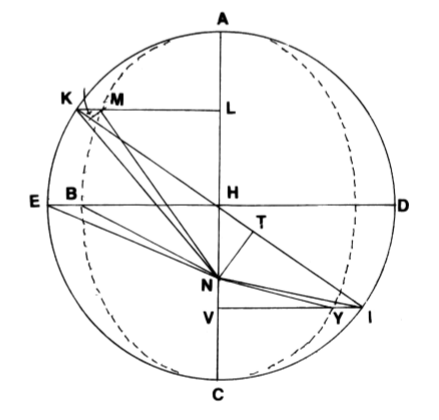
は太陽から最も離れた点で遠日点、 は太陽に最も近づいた点で近日点である。 したがって
は火星軌道の長径。
は 中心 において長軸と垂直に交わる直線。
は離心円上の点であり、 から長軸に垂線を下ろしたとき、垂線の足が、それぞれ 。
点 はそれら垂線と軌道との交点。
円の内側を走る点線は、ティコ・ブラーエ の観測値から得られた、火星の軌道と推定 される曲線である。
(以下では、二点 の距離を で表す。これは線分 の長さである)
視覚的均差とは、離心円上の点から中心 と太陽の位置 を見たときできる角のこ
とで、図では、 が
それに相当する。
いま、半径 から上方の部分の円弧
の各点における視覚的均差を考えると、それは点 において最大になる。すなわち、 をその円弧の上の任意の点とすれば、
が成立する。このとき、 であり、円弧
に限れば、これが最大の視覚的均差である。
平均的な長さとは、太陽と離心円上の点との距離の平均的な長さを意味し、それは である。
観測データより である。
ケプラーは円から三日月形を切り取る方法を考えていた。 三日月の幅が最大で であること、また最大の視覚的均差5度18分の正割が であることを契機にして、ケプラーは惑星の正しい距離が 100429 ではなく、 である、ということを推測したのである。
上の文によれば、ケプラーは偶然 5°18´のセカントを計算したところ 1.00429 を得た。一方、 の長さは、
より、 であり、次が成立す
る。
一方、ブラーエのデータ計算から
ゆえに、。これは1とみなしてよ
い。
これより、次式が成り立つ。
最後の は太陽と火星の距離を表す。
この式は、上の引用文の最後の部分:「正割 の代りに半径 を用いると、観測結果 のとおりとなる」を示すものである。
ここがケプラーの凄いところで、楕円軌道発見のきっかけになったところである。
さらに、この式は次を意味している。
平均的な長さをとる離心円上の点 において、その点と太陽との距離 に視覚的均差の余弦(コサイン)を乗じたとき、その値は火星と太陽との距離 を与える。
この命題を離心円の円弧 上の任意の点に一般化すれば、次の命題が得られよう。
離心円上の点から太陽を見たとき、その点と太陽との距離に視覚的均差の余弦を乗じたとき、その値は火星と太陽との距離を与える。
ケプラーを目覚めさせたのは、この関係である。
この命題を円弧 上の点に適用する。
図において、 をその円弧の任意の点とし、 から長軸上に垂線を下す。ここで直線 を の方に延長し、 からその直線に垂線 を下す。このとき、 における視覚的均差 とおくと、これは と同じであるが、命題から、
が火星と太陽との距離を与えると推定される。
いま、 を中心とし、半径 の円を描き、それと上の垂線 との交点を とする。
このとき、もちろん、次式が成り立つ。
いま、火星が点 を通ると仮定しよう。
ここで、 と置き、次のように推理を進める。
離心円の半径は 1 だから、
したがって
また、 のゆえ
このことは次の結果を意味する。
円弧
の任意の点 から長軸 上に垂線 を下すとき、この垂線は点 において
同一の比
に分割される。
同様な推論は中心 について点対象である円弧
においても成り立つ。
いま、 を直線 を延長したとき離心円と交わる点とする。 が円弧
の任意の点であるから、 を円弧
の任意の点とみなすことができる。 から長軸 上に垂線を下し、その足を とする。ここで、上の命題を適用すると、 とおけば、
が火星と太陽との距離を与えると推定される。
このとき、 を中心として半径 の円を描き、その円と垂線 との交点を とし、火星が の位置にあるとすれば、上の
推定から が成立する。
、 だから、
ゆえに、
これによって、点 は垂線 を前述の式と同じ比に分割する。
すなわち、点 や の集合は楕円を作る。
(注)しかしここで注意しなければならないことは、はじめから火星が点 M や Y の位置にあることは全くわからないということである。前述したようにティコ・ブラーエの観測データがいくら正確だったと言っても、直接楕円と円の形の違いを見極めて楕円軌道を発見することはできなかったのです。ケプラーが楕円軌道の決め手となった点 M や Y を選択したのは最終段階であった。こうしてケプラーは楕円軌道のアイデアをもとにあとはティコ・ブラーエの観測データから点 M や Y を確認することだった。
参考論文:都築正信(つづきまさのぶ)「ケプラーの火星楕円軌道について」(https://sucra.repo.nii.ac.jp/records/16060)

