エカント なぜ円になるか

プトレマイオスはアポロニウス，ヒッパルコスによって発展させられた離心円説，周転円説を巧みに組み合わせ観測とも調和する天動説を確立した。その際登場したのがエカント(等化点)なる不思議な点である．プトレマイオスは離心円の中心をはさんで地球のちょうど反対側にある点のことをエカントと呼んだ。 そして彼は周転円の中心はエカントに対して等速で回転するとした。

読者は、プトレマイオスのエカントがケプラーの楕円軌道における二つの焦点のうち太陽以外の焦点と同じ役割を果たしていることに気がつくだろう。この焦点から楕円軌道の惑星の動きを観測すると等速円運動を描くということである。 プトレマイオスがどのようにしてこのエカントに到達したかは定かではないが、「楕円」というものから シンプルに考えてみよう。

「楕円」は、平面上の2つの定点 F1 と F2 からの距離の和が一定となるような点 P の軌跡から作られる曲線、のことをいう。この２つの定点が「焦点」と呼ばれる。

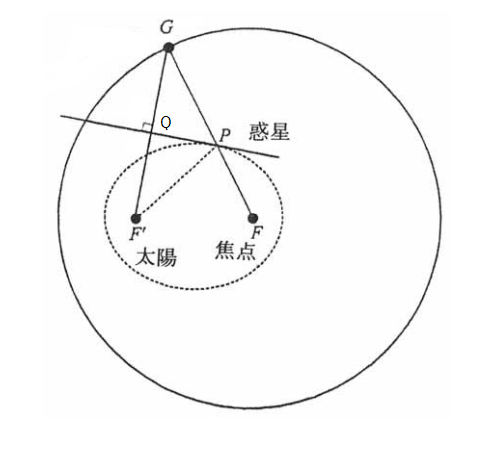
図では太陽の位置は $\text{F′}$ にあるとし、惑星は $\text{P}$ に あるとする、$\text{P}$ に楕円上で接線を引き．次にこの 接線に $\text{F′}$ より垂線を下して交点を$\text{Q}$ とし、$\text{FP}$ の延長線との交点を$\text{G}$ とすると $\text{∠F′PQ＝∠GPQ}$ より $\text{△PGQ}$ と $\text{△PF′Q}$ は合同である。したがって $\stackrel{\_}{\mathrm{PF\prime }}=\stackrel{\_}{\mathrm{PG}}$ となる．接線に対して $\text{G}$ は $\text{F′}$ の鏡像点となっている。楕円の性質により，楕円の 2 焦点 からの距離の和（$\stackrel{\_}{\mathrm{PF\prime }}+\stackrel{\_}{\mathrm{PF}}$）は一定であり，その長さは $\stackrel{\_}{\mathrm{FPG}}$ の長さに等しい。$\text{P}$ が楕円のどこに移動 してもこの関係は変わらない。よって $\text{F}$ から 見た惑星の動きは $\text{P}$ の移動につれて $\text{F}$ を中心とする円軌道を描くことになる。つまり太陽の鏡像点 $\text{G}$ は、焦点 $\text{F}$ から見た場合、惑星が天球上を等速円運動するように見えることになる。