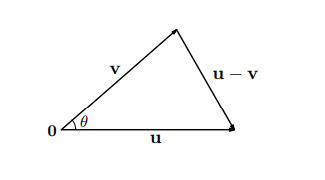線形代数(10)

ユークリッド空間上では, ユークリッド内積を考えることにより,「ベクトルの長さ」や「二つのベクトルの間の角度」といった概念を意味付けることができた。そのことを、復習を兼ねて反省してみよう。

　先ず、ベクトル

u \in R^{n}

が勝手にひとつ与えられたとして、ベクトル

u の長さ ∥ u ∥ が R^{n}

の座標を用いてどのように表わされた、かということを考えてみると、

n = 1 のときには、 u = (x) \in R^{1} として、ベクトル u の長さは ∥ u ∥=| x |= \sqrt{x^{2}} また、 n = 2 のときには、 u = (\begin{matrix} x \\ y \end{matrix}) \in R^{2} として、ベクトル u の長さは、「三平方の定理」から ∥ u ∥= \sqrt{x^{2} + y^{2}} さらに、 n = 3 のときには、 u = (\begin{matrix} x \\ y \\ z \end{matrix}) \in R^{3} を u_{1} = (\begin{matrix} x \\ y \\ 0 \end{matrix}), u_{2} = (\begin{matrix} 0 \\ 0 \\ z \end{matrix}) \in R^{3} u = u_{1} + u_{2} と分解してから、「三平方の定理」を用いると ベクトル u の長さは ∥ u ∥= \sqrt{{∥ u_{1} ∥}^{2} + {∥ u_{2} ∥}^{2}} = \sqrt{(x^{2} + y^{2}) + z^{2}} = \sqrt{x^{2} + y^{2} + z^{2}}

という式で与えられることが分かる。

　全く同様にして、勝手な自然数

n \in N

に対して、

u = (\begin{matrix} x_{1} \\ ⋮ \\ x_{n -1} \\ x_{n} \end{matrix}), u_{1} = (\begin{matrix} \begin{matrix} x_{1} \\ ⋮ \\ x_{n -1} \\ 0 \end{matrix} \end{matrix}), u_{2} = (\begin{matrix} \begin{matrix} 0 \\ ⋮ \\ 0 \\ x_{n} \end{matrix} \end{matrix}) \in R^{n} として、 R^{n} のベクトル u を u = u_{1} + u_{2} と分解してから、「三平方の定理」を用いると ベクトル u の長さは ∥ u ∥= \sqrt{{∥ u_{1} ∥}^{2} + {∥ u_{2} ∥}^{2}} = \sqrt{{∥ u_{1} ∥}^{2} + {(x_{n})}^{2}} と表わせることが分かりますから、一般に、 R^{n} のベクトル u の長さは ∥ u ∥= \sqrt{{(x_{1})}^{2} + {(x_{2})}^{2} +\dots+ {(x_{n -1})}^{2} + {(x_{n})}^{2}} \dots (1)

という式で与えられることが分かる。

　次に、

R^{n} の二つのベクトル u, v \in R^{n}

に対して、ベクトル

u

とベクトル

v

の間の角度について考えてみる。
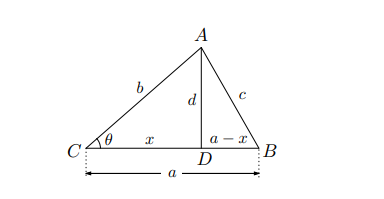
いま、平面上の三角形

Δ

ABC に対して、点 A から辺 BC に下ろした垂線の足を点 D とする。

すると、

\{\begin{matrix} d^{2} = b^{2} - x^{2} \\ d^{2} = c^{2} - {(a - x)}^{2} \end{matrix} より b^{2} - x^{2} = c^{2} - {(a - x)}^{2} 2 a x = a^{2} + b^{2} - c^{2} 一方、 x = b \cos θ より 2 a b \cos θ = a^{2} + b^{2} - c^{2} \dots (2) となることが分かる。

　そこで、いま、

R^{n} の二つのベクトル u, v \in R^{n}

に対して、ベクトル

u

とベクトル

v

の間の角度を

θ

として、

u

と

v

を二辺とする三角形に対して、いわゆる「三角形の余弦定理」(2)を適用することを考えてみると、

a = ∥ u ∥, b = ∥ v ∥, c = ∥ u - v ∥

∥ u ∥ \cdot ∥ v ∥ \cdot \cos θ = \frac{1}{2} \{{∥ u ∥}^{2} + {∥ v ∥}^{2} - {∥ u - v ∥}^{2}\} \dots (3)

いま、二つのベクトル

u, v

が座標を用いて、

u = (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix}), v = (\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{matrix}) と表わすとすると、(1)式を適用して、 {∥ u ∥}^{2} + {∥ v ∥}^{2} - {∥ u - v ∥}^{2} = \{{(x_{1})}^{2} + {(x_{2})}^{2} +\dots+ {(x_{n})}^{2}\} + \{{(y_{1})}^{2} + {(y_{2})}^{2} +\dots+ {(y_{n})}^{2}\} - \{{(x_{1} - y_{1})}^{2} + {(x_{2} - y_{2})}^{2} +\dots+ {(x_{n} - y_{n})}^{2}\} = 2 \cdot (x_{1} y_{1} + x_{2} y_{2} +\dots+ x_{n} y_{n})

と表わせることが分かる。

以上の考察より、

R^{n}

上の標準的なユークリッド内積

{⟨ , ⟩}_{R^{n}}

は、座標を用いて、

{⟨ u, v ⟩}_{R n} = x_{1} y_{1} + x_{2} y_{2} +\dots+ x_{n} y_{n} = \sum_{k = 1}^{n} x_{k} y_{k} \dots (4)

というように表わせることが分かる。
　すると、

R^{n}

上の標準的なユークリッド内積

{⟨ , ⟩}_{R^{n}}

は、次のような基本的な性質、

(イ)　双線型性：勝手なベクトル

u, u^{'}, v, v^{'} \in R^{n}

と勝手な実数　

c \in R

に対して

\{\begin{matrix} {⟨ u + u^{'}, v ⟩}_{R^{n}} = {⟨ u, v ⟩}_{R^{n}} + {⟨ u^{'}, v ⟩}_{R^{n}} \\ {⟨ c u, v ⟩}_{R^{n}} = c \cdot {⟨ u, v ⟩}_{R^{n}} \end{matrix} \{\begin{matrix} {⟨ u, v + v^{'} ⟩}_{R^{n}} = {⟨ u, v ⟩}_{R^{n}} + {⟨ u, v^{'} ⟩}_{R^{n}} \\ {⟨ u, c v ⟩}_{R^{n}} = c \cdot {⟨ u, v ⟩}_{R^{n}} \end{matrix}

(ロ)　対称性 : 勝手なベクトル

u,, v \in R^{n}

に対して

{⟨ u, v ⟩}_{R^{n}} = {⟨ v, u ⟩}_{R^{n}}

(ハ)　正値性 : 勝手なベクトル

u \in R^{n}

に対して

{⟨ u, u ⟩}_{R^{n}} \geq 0 かつ、 {⟨ u, u ⟩}_{R^{n}} = 0 \Leftrightarrow u = O

という三つの性質を持つことが分かる。例えば、(イ) の線型性は (4)式より

⟨ u + u^{'}, v ⟩ = \sum_{k = 1}^{n} (x_{k} + {x^{'}}_{k}) \cdot y_{k} = \sum_{k = 1}^{n} x_{k} y_{k} + \sum_{k = 1}^{n} x_{k}^{'} y_{k} = ⟨ u, v ⟩ + ⟨ u^{'}, v ⟩ その他の性質も、同様の考察を行なうことで確認することができる。

特に、(ハ)より、

R^{n}

上の標準的なユークリッド内積に関するベクトル

u \in R^{n}

の長さは、

∥ u ∥ = \sqrt{{⟨ u, u ⟩}_{R^{n}}}

というように表わせることも分かる。

そこで、これらの

R^{n}

上の標準的なユークリッド「内積の概念」を、

R

上の線型空間 V 上の内積

{⟨, ⟩}_{V}

に拡張して、(イ)(ロ)(ハ) を

{⟨, ⟩}_{R^{n}} から {⟨, ⟩}_{V}

に置き換えて、これらの条件を満たすときに、線型空間 V 上の内積と呼ぶ。

すると、内積を持つ線型空間 (

V, {⟨ , ⟩}_{V}) の元 u \in V

の長さは、

∥ u ∥ = \sqrt{{＜ u, u ＞}_{V}}

という式によって定めることができることが分かる。また、

u, v \in V, t \in R

として

t u + v \in V という元に対して、(ハ)という条件を当てはめてみると、 0 \leq {⟨ t u + v, t u + v ⟩}_{V} = t^{2} \cdot {⟨ u, u ⟩}_{V} + t \cdot {⟨ u, v ⟩}_{V} + t \cdot {⟨ v, u ⟩}_{V} + {⟨ v, v ⟩}_{V} = {∥ u ∥}^{2} \cdot t^{2} + 2 {⟨ u, v ⟩}_{V} \cdot t + {∥ v ∥}^{2}

これが、勝手な実数

t \in R

に対して成り立つためには、右辺に現われる二次式の判別式

D は D \leq 0

でなければならないから、

{{⟨ u, v ⟩}_{V}}^{2} \leq {∥ u ∥}^{2} \cdot {∥ v ∥}^{2} よって | {⟨ u, v ⟩}_{V} | \leq ∥ u ∥ \cdot ∥ v ∥ \dots (5)

となることが分かる。この(5)式を Schwarz の不等式　と呼ぶ。

そこで、Schwarz の不等式を用いると、

{⟨ u, v ⟩}_{V} = ∥ u ∥ \cdot ∥ v ∥ \cdot \cos θ

となるような実数

θ \in R

が存在することが分かるから, このような実数

θ

として, 二つの元

u と v

のなす角度が定義できることが分かる。
すると、線型空間 V の元の「長さ」や二つの元のなす「角度」も, ユークリッド空間上のベクトルの「長さ」や二つのベクトルのなす「角度」としてイメージすることができる。すなわち、、線型空間 V　に正規直交基底を用いて線型空間 V を「番地割り」して考えることにすると、

(V, {⟨, ⟩}_{V}) ≅ (R^{n}, {⟨, ⟩}_{R^{n}})

というように同一視ができることになる。

さて、いま、二つのベクトル

u, v

が座標を用いて、

u = (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}), v = (\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \end{matrix})

と表わされているとする。また、3 行 3 列の勝手な行列 A　が

A = (\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix})

ひとつ与えられているとする。
　このとき、内積

⟨ A u, v ⟩ と ⟨ u, A v ⟩

を考えてみよう。

先ず、内積 ⟨ A u, v ⟩ は ⟨ A u, v ⟩ = ⟨ [(\begin{matrix} a_{11} x_{1} + a_{12} x_{2} + a_{13} x_{3} \\ a_{21} x_{1} + a_{22} x_{2} + a_{23} x_{3} \\ a_{31} x_{1} + a_{32} x_{2} + a_{33} x_{3} \end{matrix}), (\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \end{matrix})] ⟩ = (a_{11} x_{1} + a_{12} x_{2} + a_{13} x_{3}) y_{1} + (a_{21} x_{1} + a_{22} x_{2} + a_{23} x_{3}) y_{2} + (a_{31} x_{1} + a_{32} x_{2} + a_{33} x_{3}) y_{3} \dots (6) 一方、内積 ⟨ u, A v ⟩ は ⟨ u, A v ⟩ = ⟨ [(\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}), (\begin{matrix} a_{11} y_{1} + a_{12} y_{2} + a_{13} y_{3} \\ a_{21} y_{1} + a_{22} y_{2} + a_{23} y_{3} \\ a_{31} y_{1} + a_{32} y_{2} + a_{33} y_{3} \end{matrix})] ⟩ = x_{1} (a_{11} y_{1} + a_{12} y_{2} + a_{13} y_{3}) + x_{2} (a_{21} y_{1} + a_{22} y_{2} + a_{23} y_{3}) + x_{3} (a_{31} y_{1} + a_{32} y_{2} + a_{33} y_{3}) = (a_{11} x_{1} + a_{21} x_{2} + a_{31} x_{3}) y_{1} + (a_{12} x_{1} + a_{22} x_{2} + a_{32} x_{3}) y_{2} + (a_{13} x_{1} + a_{23} x_{2} + a_{33} x_{3}) y_{3} \dots (7)

(6)、(7)式より、勝手な実数

c \in R

に対して成り立つ(イ)の双線型性、

{⟨ c u, v ⟩}_{R^{n}} = {⟨ u, c v ⟩}_{R^{n}}

行列では成り立たない（

⟨ A u, v ⟩ \neq ⟨ u, A v ⟩

）、ということが分かる。
このことをよくよく考えると、、内積

{⟨ u, v ⟩}_{R^{n}}

は、行列の積を用いて

⟨ u, v ⟩ = (\begin{matrix} x_{1} & x_{2} & \dots & x_{n} \end{matrix}) (\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{matrix}) = {}^{t}u \cdot v \dots (8)

というように表わすことができることに注意する。
　そこで、

A u と v

の間の内積

⟨ A u, v ⟩ を考えてみると、 ⟨ A u, v ⟩ は

⟨ A u, v ⟩ = {}^{t}{(A u)} \cdot v = {}^{t}u {}^{t}A \cdot v = {}^{t}u \cdot {}^{t}A v = ⟨ u, {}^{t}A v ⟩ したがって、 ⟨ A u, v ⟩ = ⟨ u, {}^{t}A v ⟩ \dots (9)

となることが分かる。

そこで、

⟨ A u, v ⟩ = ⟨ u, B v ⟩ {}^{\forall}u, v \in R^{n} \dots (10) となるような行列、もちろん、 B = {}^{t}A

とすれば、(10)式が成り立つことは分かるが、(10)式を満たす行列

B は {}^{t}A

だけだろうか。
いま、(10)式を満たす行列　

B

が見つかったと仮定してみよう。すると、内積はスカラーであり、線型性をもつから、(10)式から(9)式を引き算してみると

0 = ⟨ u, B v ⟩ - ⟨ u, {}^{t}A v ⟩ = ⟨ u, B v - {}^{t}A v ⟩ = ⟨ u, (B - {}^{t}A) v ⟩ となることから、 ⟨ u, (B - {}^{t}A) v ⟩ = 0 これが、勝手なベクトル、 u \in R^{n} に対して、成り立つから (B - {}^{t}A) v = 0 さらに、勝手なベクトル、 v \in R^{n} に対しても、成り立つから B - {}^{t}A = 0

でなければならないことが分かる。

以上から、与えられた行列　

A

に対して、(10)式を満たすような行列

B

は、

B = {}^{t}A

しか存在しない、ということが分かる。すなわち、行列 A に対して, その転置行列

{}^{t}A

は、(10)式を満たすような行列として一意的に特徴付けられる。

線形代数(10)

≪線形空間の「内積」構造≫