Document

行列に対する基本的な概念として「行列式」というものがあるが、そもそも「行列式」とはなんだろうか？
行列式になぜ「置換」や「置換の符号」というのが出てくるのか？
「行列の故郷」に帰って考えてみよう。

いま、方程式が

A X = B

……(1)

とすると、この問題は「 A 倍すると B となる数 X は？」という問題と解釈できることになるから　

A \neq 0 ならば X = \frac{B}{A} \dots (2)

として、簡単に解くことができる。

そこで、さらに

a x + b y = e \dots (3) c x + d y = f \dots (4)

のように与えられている、とすると、この連立方程式は、

(3) * d - (4) * b (a \cdot d - c \cdot b) x + (b \cdot d - d \cdot b) y = (e \cdot d - f \cdot b) したがって (a \cdot d - c \cdot b) x = (e \cdot d - f \cdot b) \dots (5)

同様にして

(4) * a - (3) * c (c \cdot a - a \cdot c) x + (d \cdot a - b \cdot c) y = (f \cdot a - e \cdot c) したがって (d \cdot a - b \cdot c) y = (f \cdot a - e \cdot c) \dots (6)

いま、

(a d - b c) \neq 0

ならば、(5),(6)式より

x = \frac{e d - f b}{a d - b c} y = \frac{f a - e c}{a d - b c}

として、

x, y

　を一意に求めることができる。ここで、

(a d - b c) \neq 0

が重要な条件になっていることに注意する。

ところで、上の連立方程式を「行列」の記法で書き表わすと

(\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} e \\ f \end{matrix}) \dots (7) そこで、 A = (\begin{matrix} a & b \\ c & d \end{matrix}) u = (\begin{matrix} x \\ y \end{matrix}) b = (\begin{matrix} e \\ f \end{matrix}) と表わすことにすると、(7)式の連立一次方程式は A u = b \dots (8) というように、簡明な形で表わすことができる。

すると、(8)式は「

A 倍すると b となる数 u は何か？

」という問題と解釈できるから、

u = \frac{b}{A}

……(9)

となるのではないかと「当たり」が付く。
しかし、ここでも　

A \neq 0

ということが、絶対的な条件となる。すなわち、

A

の「或る数値」がゼロであるか、そうでないか、ということが決定因子(determinant)になる。そこで「或る数値」を　det

A

と呼ぶことにすると、ある正方行列　

A

　に対して「或る数値」　det

A

　を対応させることができ、この関数を「行列式」と呼び、det

A

または　

| A |

と表記する。

ところで、行列の世界では、掛け算の結果は、一般には、積の順番に依ってしまうから

二つの行列 A, B に対して A^{-1} B と B A^{-1} が

等しいとは限らない。
したがって、

\frac{B}{A}

という記法を使用すると、

\frac{B}{A} = A^{-1} B と解釈するか、 \frac{B}{A} = B A^{-1} と解釈するか、

によって、

\frac{B}{A}

が表わす行列が異なってしまうというような混乱が生じ得る。このような理由で、行列の世界では「分数」の記法は用いずに　

A^{-1}

というように「負ベキ」の指数を用いて、「右から」「左から」を明確にして、「分数」を表わす。

したがって、(8)式から(9)式への変形は、正確には次のようになる。

\det A \neq 0 ならば A^{-1} A u = u = A^{-1} b

すると、(7)式の連立一次方程式を解く問題は、「方程式の「係数」である行列 A の逆行列

A^{-1}

を求める問題」に取って代わるように見える。

行列式が意味するもの

一般に、n 行 n 列の行列 A に対して, 行列式と呼ばれる数を対応させることができる。
そこで、n=2　2行2列の正方行列 A の場合で考えてみよう。
いま、

(\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}) (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})

は、

(\begin{matrix} 1 \\ 0 \end{matrix}) を (\begin{matrix} 1 \\ 3 \end{matrix}) に写し (\begin{matrix} 0 \\ 1 \end{matrix}) を (\begin{matrix} 2 \\ 4 \end{matrix}) に写す。

そこで、

A = (\begin{matrix} a & b \\ c & d \end{matrix}) を a_{1} = (\begin{matrix} a \\ c \end{matrix}), a_{2} = (\begin{matrix} b \\ d \end{matrix}) として A を A = (a_{1}, a_{2}) のように

列ベクトルが並んだものとして考えてみよう。

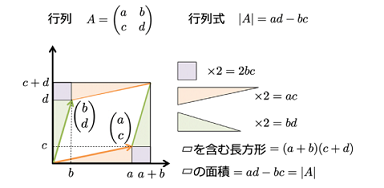
すると、行列式とは、平面

R^{2}

上の二つのベクトル　

a_{1}, a_{2} \in R^{2}

に対して、何か数を対応させる関数　

f (a_{1}, a_{2})

である、といえる。それでは、上の方程式(5),(6)式で現れた　

(a d - b c)

が意味するものは何だろうか。そこで, 逆に,「平面上の二つのベクトルを与えたときに, 自然に定まるような数とは何だろうか」ということを考えてみる。いろんなものがあると思うが、二つのベクトルでできる平行四辺形の面積を考える、というのは、ごく自然な発想であろう。実際に　

(a d - b c)

は面積を表している。

(a + b) (c + d) - (a c + b d + 2 b c) = a d - b c

そこで、二つのベクトル（

a_{1}, a_{2}

）でできる平行四辺形の面積を対応させる関数を

S (a_{1}, a_{2})

　と書くことにする。そして、ひとつだけ次のような取り決めを行う。

a_{1}, a_{2} \in R

から定まる平行四辺形の普通の意味での(正の)面積を

| S (a_{1}, a_{2}) |

というように絶対値を付けて表わした場合、
　(1)

a_{1} から見て、 a_{2}

が反時計回りにに 180度回転するまでに得られる方向にあるとき

S (a_{1}, a_{2}) = | S (a_{1}, a_{2}) |

　(2)

a_{1} から見て、 a_{2}

が時計回りにに 180度回転するまでに得られる方向にあるとき

S (a_{1}, a_{2}) = -| S (a_{1}, a_{2}) |

　例えば、

a_{1}

を勝手にひとつ固定して、

a_{2}

を長さを保ったまま、

a_{1}

の定める方向から始めて、反時計回りに回転させてゆくときの符号つきの面積　

S (a_{1}, a_{2})

の変化を考えると、最初は正の面積が段々増えてゆき、

a_{2} が a_{1}

と直交する方向を向いたときに面積が最大になり、その後、正の面積は段々減って　

a_{2} が a_{1}

　と反対の方向に向いたときに面積が 0 となり、その後は、面積が負となり、同様の変化をするというように解釈する。

そこで、このように符号つきで面積を考えたときに　

S (a_{1}, a_{2})

という関数はどのような性質をもつだろうか。
　まず、

a_{1}, a_{1}^{'}, a_{2} \in R^{2}

とすると、ベクトル

a_{1} + a_{1}^{'} と a_{2}

でできる平行四辺形の面積

S (a_{1} + a_{1}^{'}, a_{2})

　はどのように変化するだろうか。そのため、

a_{1}, a_{1}^{'}, a_{1} + a_{1}^{'} \in R^{2} などから、 a_{2}

を延長して得られる直線に垂線を下ろして、それらの高さを、それぞれ　

h_{1}, h_{1}^{'}, h_{1}^{''}

とすると、

h_{1}^{''} = h_{1} + h_{1}^{'} となるから、 a_{2} の長さを l_{2} とすると 平行四辺形の面積 = 高さ \times 底辺  より h_{1}^{''} \cdot l_{2} = (h_{1} + h_{1}^{'}) \cdot l_{2} = h_{1} \cdot l_{2} + h_{1}^{'} \cdot l_{2} したがって、 S (a_{1} + a_{1}^{'}, a_{2}) = S (a_{1}, a_{2}) + S (a_{1}^{'}, a_{2}) となることが分かる。

　さらに、

a_{1}, a_{2} \in R^{2}, c \in R として、 S (c \cdot a_{1}, a_{2})

を考えてみた場合、

c \geq 0

のときには、

a_{1} と同じ向きに a_{1}

　の長さが c 倍されることになるから、平行四辺形は向きを保ったまま、面積が c 倍されることになり

S (c \cdot a_{1}, a_{2}) = c \cdot S (a_{1}, a_{2})

となることが分かる。一方、

c \leq 0

のときには、

a_{1} と向きを逆にして a_{1}

　の長さが |c| 倍されることになるから、平行四辺形は向きを逆にして、面積が |c|倍されることになり

S (c \cdot a_{1}, a_{2}) = -| c |\cdot S (a_{1}, a_{2}) = c \cdot S (a_{1}, a_{2})

以上から、関数

S (a_{1}, a_{2}) は a_{1}

という変数に関して線形写像になっていることが分かる。全く同様にして、関数

S (a_{1}, a_{2}) は a_{2}

という変数に関しても線形写像になっていることが分かるから、関数

S (a_{1}, a_{2})

は「多重線形性」という性質をもつ。

また、一方、関数

S (a_{1}, a_{2}) と、関数 S (a_{2}, a_{1})

　を比較した場合、すなわち、関数

S (a_{1}, a_{2}) の変数、ベクトル a_{1} と a_{2}

を取り替えた場合は、取り決めにより、向きが逆になることになるから、

S (a_{1}, a_{2}) =- S (a_{2}, a_{1})

となることが分かる。すなわち「歪対称性」の性質をもつ。
特に、

a_{1} = a_{2} とすると f (a_{1}, a_{1}) =- f (a_{1}, a_{1}) 2 f (a_{1}, a_{1}) = 0 f (a_{1}, a_{1}) = 0

これまでの考察では、2 行 2 列の行列

A = (\begin{matrix} a & b \\ c & d \end{matrix})

が、勝手にひとつ与えられているとして、これを、

a_{1} = (\begin{matrix} a \\ c \end{matrix}), a_{2} = (\begin{matrix} b \\ d \end{matrix})

という二つのベクトルが与えられたと解釈して、

S (a_{1}, a_{2})

という関数がどのような性質をもつのか、ということを考察し、
(イ)　多重線形性
(ロ)　歪対称性
という性質をもつことを確認した。
　そこで、(イ),(ロ)という２つの性質だけを認めることで　

f (a_{1}, a_{2})

という関数の形はどこまで定まるのか、ということを見てみよう。

いま、

e_{1} = (\begin{matrix} 1 \\ 0 \end{matrix}), e_{2} = (\begin{matrix} 0 \\ 1 \end{matrix}) \in R^{2} とすると、 a_{1} は、 a_{1} = (\begin{matrix} a \\ c \end{matrix}) = a \cdot (\begin{matrix} 1 \\ 0 \end{matrix}) + c \cdot (\begin{matrix} 0 \\ 1 \end{matrix}) = a \cdot e_{1} + c \cdot e_{2} と書き表わせ、代入して、さらに(イ)を用いると f (a_{1}, a_{2}) = f (a \cdot e_{1} + c \cdot e_{2}, a_{2}) = f (a \cdot e_{1}, a_{2}) + f (c \cdot e_{2}, a_{2}) = a \cdot f (e_{1}, a_{2}) + c \cdot f (e_{2}, a_{2}) \dots (10) さらに、 a_{2} = b \cdot e_{1} + d \cdot e_{2} として、(10)式に代入すると f (a_{1}, a_{2}) = a \cdot f (e_{1}, b \cdot e_{1} + d \cdot e_{2}) + c \cdot f (e_{2}, b \cdot e_{1} + d \cdot e_{2}) = a b \cdot f (e_{1}, e_{1}) + a d \cdot f (e_{1}, e_{2}) + c b \cdot f (e_{2}, e_{1}) + c d \cdot f (e_{2}, e_{2}) \dots (11) ここで、(ロ)という性質を用いると f (e_{1}, e_{1}) = f (e_{2}, e_{2}) = 0 f (e_{1}, e_{2}) = - f (e_{2}, e_{1}) (11)式は、結局 f (a_{1}, a_{2}) = (a d - b c) \cdot f (e_{1}, e_{2}) \dots (12) というように書き換えられることが分かる。

すなわち、(イ),(ロ)という二つの性質を持つような関数は、

f (e_{1}, e_{2})

の値を何にするか、という定数倍の不定性を除いて、(12)式のように、その関数の形が決まってしまうことが分かる。

ところで、

e_{1}, e_{2}

を二辺とする平行四辺形は、正の向きを持つ、一辺が 1 の正方形になるから、

f (e_{1}, e_{2}) = 1

したがって、(ハ)　規格化条件が成り立つ。

以上から、(イ),(ロ),(ハ)という三つの性質をもつ関数は、

f (a_{1}, a_{2}) = a d - b c

というように, 唯一通りに関数の形が定まってしまうことが分かる。

これまでの考察で、n=2 のとき、行列式とは「符号つきの面積を対応させる関数」であり、このような関数は (イ),(ロ),(ハ)という三つの性質

(イ)　多重線形性：

\forall a_{1}, a_{1}^{'}, a_{2}, a_{2}^{'} \in R^{2}, \forall c \in R に対して、 つぎが成り立つ。 \{\begin{matrix} f (a_{1} + a_{1}^{'}, a_{2}) = f (a_{1}, a_{2}) + f (a_{1}^{'}, a_{2}) \\ f (c \cdot a_{1}, a_{2}) = c \cdot f (a_{1}, a_{2}) \end{matrix} \{\begin{matrix} f (a_{1}, a_{2} + a_{2}^{'}) = f (a_{1}, a_{2}) + f (a_{1}, a_{2}^{'}) \\ f (a_{1}, c \cdot a_{2}) = c \cdot f (a_{1}, a_{2}) \end{matrix}

(ロ)　歪対称性：

\forall a_{1}, a_{2} \in R^{2} に対して、 つぎが成り立つ。 f (a_{1}, a_{2}) =- f (a_{2}, a_{1}) (f (a_{1}, a_{1}) = 0)

(ハ)　規格化条件：

e_{1} = (\begin{matrix} 1 \\ 0 \end{matrix}), e_{2} = (\begin{matrix} 0 \\ 1 \end{matrix}) に対して、 つぎが成り立つ。 f (e_{1}, e_{2}) = 1

で一意的に特徴づけられる、ということが分かった。

それでは、n=3 の場合はどうなるであろうか。
　いま、3行3列の行列

A = (\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix})

が与えられているとして A の列ベクトルを

a_{1} = (\begin{matrix} a \\ d \\ g \end{matrix}), a_{2} = (\begin{matrix} b \\ e \\ h \end{matrix}), a_{3} = (\begin{matrix} c \\ f \\ i \end{matrix}) と表わし e_{1} = (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}), e_{2} = (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}), e_{3} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) と表わすことにする。 すると、 a_{1}, a_{2}, a_{3} は、それぞれ、 \{\begin{matrix} a_{1} = a \cdot e_{1} + d \cdot e_{2} + g \cdot e_{3} \\ a_{2} = b \cdot e_{1} + e \cdot e_{2} + h \cdot e_{3} \\ a_{3} = c \cdot e_{1} + f \cdot e_{2} + i \cdot e_{3} \end{matrix} と表わすことができる。

そこで、n=2 の場合と同様に、(イ)の「多重線形性」だけを用いて、

f (a_{1}, a_{2}, a_{3})

を書き換えてみると、

f (a_{1}, a_{2}, a_{3}) = a b c \cdot f (e_{1}, e_{1}, e_{1}) + a b f \cdot f (e_{1}, e_{1}, e_{2}) + a b i \cdot f (e_{1}, e_{1}, e_{3}) + a e c \cdot f (e_{1}, e_{2}, e_{1}) + a e f \cdot f (e_{1}, e_{2}, e_{2}) + a e i \cdot f (e_{1}, e_{2}, e_{3}) + a h c \cdot f (e_{1}, e_{3}, e_{1}) + a h f \cdot f (e_{1}, e_{3}, e_{2}) + a h i \cdot f (e_{1}, e_{3}, e_{3})

+ d b c \cdot f (e_{2}, e_{1}, e_{1}) + d b f \cdot f (e_{2}, e_{1}, e_{2}) + d b i \cdot f (e_{2}, e_{1}, e_{3}) + d e c \cdot f (e_{2}, e_{2}, e_{1}) + d e f \cdot f (e_{2}, e_{2}, e_{2}) + d e i \cdot f (e_{2}, e_{2}, e_{3}) + d h c \cdot f (e_{2}, e_{3}, e_{1}) + d h f \cdot f (e_{2}, e_{3}, e_{2}) + d h i \cdot f (e_{2}, e_{3}, e_{3})

+ g b c \cdot f (e_{3}, e_{1}, e_{1}) + g b f \cdot f (e_{3}, e_{1}, e_{2}) + g b i \cdot f (e_{3}, e_{1}, e_{3}) + g e c \cdot f (e_{3}, e_{2}, e_{1}) + g e f \cdot f (e_{3}, e_{2}, e_{2}) + g e i \cdot f (e_{3}, e_{2}, e_{3}) + g h c \cdot f (e_{3}, e_{3}, e_{1}) + g h f \cdot f (e_{3}, e_{3}, e_{2}) + g h i \cdot f (e_{3}, e_{3}, e_{3})

という２７個の項に分解される。
そこで、(ロ)の「歪対称性」という性質を用いると、

f (e_{1}, e_{1}, e_{3})

のように、同じベクトルが重複して現われるような項は 0 になってしまうから、ベクトルが単独で現れる６個の項だけが残り、

f (a_{1}, a_{2}, a_{3}) = a e i \cdot f (e_{1}, e_{2}, e_{3}) + a h f \cdot f (e_{1}, e_{3}, e_{2}) + d b i \cdot f (e_{2}, e_{1}, e_{3}) + d h c \cdot f (e_{2}, e_{3}, e_{1}) + g b f \cdot f (e_{3}, e_{1}, e_{2}) + g e c \cdot f (e_{3}, e_{2}, e_{1})

となることが分かる。
さらに、勝手な二つのベクトルを入れ替えると (−1) 倍されるという (ロ) の性質を用いると、

f (e_{1}, e_{2}, e_{3}) =- f (e_{1}, e_{3}, e_{2}) (e_{2} \Leftrightarrow e_{3}) =- f (e_{2}, e_{1}, e_{3}) (e_{1} \Leftrightarrow e_{2}) =- f (e_{3}, e_{2}, e_{1}) (e_{1} \Leftrightarrow e_{3}) = f (e_{2}, e_{3}, e_{1}) (e_{1} \Leftrightarrow e_{3}) \to (e_{2} \Leftrightarrow e_{3}) = f (e_{3}, e_{1}, e_{2}) (e_{1} \Leftrightarrow e_{3}) \to (e_{2} \Leftrightarrow e_{1})

したがって、最終的には、

f (a_{1}, a_{2}, a_{3}) = (a e i + g b f + d h c - a h f - d b i - g e c) \cdot f (e_{1}, e_{2}, e_{3})

という形に書き直すことができる。すなわち、n=2 の場合と同様に、(イ),(ロ)という二つの性質を持つような関数は「

f (e_{1}, e_{2}, e_{3})

　の値を何にするか」という定数倍の不定性を除いて、その関数の形が決まってしまうことが分かる。
そこでさらに、(ハ)というう規格化条件　

f (e_{1}, e_{2}, e_{3}) = 1

が成り立っているから

f (a_{1}, a_{2}, a_{3}) = a e i + g b f + d h c - a h f - d b i - g e c

というように、唯一通りに関数の形が定まってしまうことが分かる。

ここまでくると、一般に、n 行 n 列の行列の場合にどうなりそうかということが予想がつく。
　いま、行列 A の

i 行 j 列の成分を a_{i j}

と表わすことにすると、行列 A の列ベクトル、

a_{1} = (\begin{matrix} a_{11} \\ a_{21} \\ ⋮ \\ a_{n 1} \end{matrix}), a_{2} = (\begin{matrix} a_{12} \\ a_{22} \\ ⋮ \\ a_{n 2} \end{matrix}), \dots, a_{n} = (\begin{matrix} a_{1 n} \\ a_{2 n} \\ ⋮ \\ a_{n n} \end{matrix}) は、それぞれ k = 1,2,3, \dots, n として a_{k} = [\begin{matrix} a_{1 k} \\ a_{2 k} \\ ⋮ \\ a_{n k} \end{matrix}] = [\begin{matrix} a_{1 k} \\ 0 \\ ⋮ \\ 0 \end{matrix}] + [\begin{matrix} 0 \\ a_{2 k} \\ ⋮ \\ 0 \end{matrix}] +\dots+ [\begin{matrix} 0 \\ 0 \\ ⋮ \\ a_{n k} \end{matrix}] = \sum_{i_{k} = 1}^{n} a_{i_{k} k}

と、書き表わすことができる。
さらに、

e_{1} = (\begin{matrix} 1 \\ 0 \\ ⋮ \\ 0 \end{matrix}), e_{2} = (\begin{matrix} 0 \\ 1 \\ ⋮ \\ 0 \end{matrix}),\dots, e_{n} = (\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \end{matrix})

を用いると、

a_{k} = a_{1 k} e_{1} + a_{2 k} e_{2} +\dots+ a_{n k} e_{n} = \sum_{i k = 1}^{n} a_{i_{k} k} e_{i_{k}}

と分解して書き表わすことができる。
　そこで、これを用いて、

f (a_{1} a_{2} \dots a_{n})

を考えると、

f (a_{1} a_{2} \dots a_{n}) = f (\sum_{i_{1} = 1}^{n} a_{i_{1} 1} e_{i_{1}} \sum_{i_{2} = 1}^{n} a_{i_{2} 2} e_{i_{2}} \dots \sum_{i_{n} = 1}^{n} a_{i_{n} n} e_{i_{n}}) (多重線形性: f (c \cdot a_{1}, a_{2}) = f (a_{1}, c \cdot a_{2}) = c \cdot f (a_{1}, a_{2}) より) = \sum_{i_{1} = 1}^{n} a_{i_{1} 1} \cdot f (e_{i_{1}} \sum_{i_{2} = 1}^{n} a_{i_{2} 2} e_{i_{2}} \dots \sum_{i_{n} = 1}^{n} a_{i_{n} n} e_{i_{n}}) = \sum_{i_{1} = 1}^{n} a_{i_{1} 1} \sum_{i_{2} = 1}^{n} a_{i_{2} 2} \cdot f (e_{i_{1}} e_{i_{2}} \dots \sum_{i_{n} = 1}^{n} a_{i_{n} n} e_{i_{n}}) ⋮ = \sum_{i_{1} = 1}^{n} a_{i_{1} 1} \sum_{i_{2} = 1}^{n} a_{i_{2} 2} \dots \sum_{i_{n} = 1}^{n} a_{i_{n} n} \cdot f (e_{i_{1}} e_{i_{2}} \dots e_{i_{n}}) = \sum_{(i_{1} i_{2} \dots i_{n}) = 1}^{n} a_{i_{1} 1} a_{i_{2} 2} \dots a_{i_{n} n} \cdot f (e_{i_{1}} e_{i_{2}} \dots e_{i_{n}}) \dots (13)

したがって、それぞれが 1 から n までとるから、、

n^{n}

個の項の和の形に書き直すことができる。
　ところで、(ロ)の歪対称性の性質から同じベクトルがあると、

f (e_{i_{1}} e_{i_{2}} \dots e_{i_{n}}) = 0

となるから、n 個ある

e_{i_{k}}

はそれぞれ1回だけ顔を出すことになる。すなわち、異なる n 個の中から1個だけ取り出す「並び替え問題」に帰着する。すると

n^{n} 個のうち、 e_{1}, e_{2},\dots, e_{n}

を入れ替えたような形をした　n! 個の項だけが残ることになる。
さらに、(ロ)のベクトルを入れ替えると(-1)倍される、という性質を用いると、並び替えた回数を t とすると　

{(-1)}^{t}

倍されることになる。そこで、

e_{i_{1}} e_{i_{2}} \dots e_{i_{n}} を e_{1}, e_{2},\dots, e_{n}

という順番に並び替えたときに現われる符号を

sgn σ \in{\pm 1}

とすると

f (e_{i_{1}} e_{i_{2}} \dots e_{i_{n}}) = sgn σ \cdot f (e_{1} e_{2} \dots e_{n})

と、表わすことができる。したがって、(14)式は最終的には

f (a_{1} a_{2} \dots a_{n}) =(\sum_{*} sgn σ \cdot a_{i_{1} 1} a_{i_{2} 2} \dots a_{i_{n} n})\cdot f (e_{1} e_{2} \dots e_{n}) (*: i_{1} \neq i_{2} \neq\dots\neq i_{n})

さらに、(ハ)の規格化条件を用いると、結局、

f (a_{1} a_{2} \dots a_{n}) = \sum_{*} sgn σ \cdot a_{i_{1} 1} a_{i_{2} 2} \dots a_{i_{n} n} \dots (14) (*: i_{1} \neq i_{2} \neq\dots\neq i_{n})

というように完全に値が定まってしまうことが分かる。

さて、ここまで考察を進めた後で、思考の順序を逆転させて、こうした考察をすべて背景に押しやってしまい、逆に、(14) 式のような表示を行列式の定義として採用することで、「 (14) 式により定義された行列式という関数が, (イ), (ロ), (ハ) という三つの性質を持つということを証明する」という形で議論することもできる。むしろ、このように議論した方が,「体積」とか「向き」とかいう概念を持ち出さずに,「論理的にすっきりした形で議論できる」という理由から、普通、線型代数学の教科書には, そのような書き方がされている。
そこで、行列式をきちんと定義するために,「置換」や「置換の符号」といった余り馴染みのない概念が最初に議論されていたり, 行列式に関する様々な性質が次から次へと述べられていたりするために,「行列式は何をやっているのか良く分からない」という印象が先立つことになる。

線形代数(15)

≪行列式とはなにか≫

行列式が意味するもの